老师解密托福加试题目

　　在TOEFL考试的阅读和听力部分中，有的考生可能会面临出现多一篇文章的情况，中国大陆将该情况称之为加试。在ETS的众多已发表文献中，我们已经可以探索出"加试"的目的。本文结合自1970年至今来ETS发布的研究报告和尚未解密的数据清楚的阐释加试的定义，目的，和实际作用。

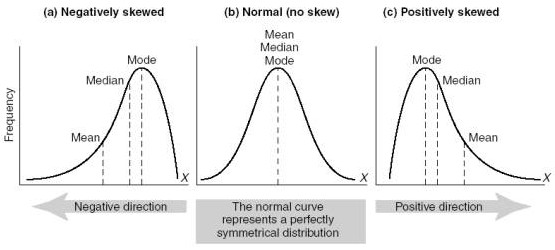
　　加试部分的官方名字叫做"Normalizing Part"，其目的是为了normalize the test。TOEFL采用的是norm-referenced 而不是criterion-referenced 评分标准，GRE也是如此，也就意味着每次的考试成绩分布应该如(B)图所示，简单来说，TOEFL是典型的high-stake standardized test，多次考试的成绩应保持一致。举例来说，2013年9月1日和9月7日的中国大陆平均成绩应保持一致，因为如果没有证据显示样本能力有显著提高，短期之内总样本量的平均成绩应该没有太大变化。可是事实上，每一次考试的数据都会有所变化，成绩分布有可能出现(A)情况-即大多数考生成绩过高(并不意味着试题难度简单)，也有可能出现(C)情况-即大多数考生成绩过低(并不意味着试题过于困难)。

　　TOEFL考试需要保持其Construct Reliability 需要其每一次考试都将整体考试的数据进行normalize，其采用的是item response theory (IRT) framework，每次考试的主体题目不同，只有加试部分一致，因此加试相当于一个 "Anchor block"来equating整体考试的成绩。因此，TOEFL考试你会得到一个raw score，你的这个成绩会放在整体数据图表中形成一个curve, 整个curve会slightly skewed，根据加试的anchor，所有考生会被normalize, 以得到一个最后的scaled score。A考生在9月1日的100分和9月7日的100分并不意味着做对了同等数量的题目。加试的目的只在于保证多次考试之间的reliability，并不对个人考生有所影响。

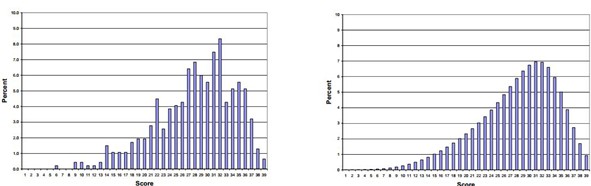
　　下面是一个702个test-taker的数据，左图为raw score, 右图为normalized过的scaled score：

　　下图对比了加试部分对于真实成绩的影响，左图为strongly correlated, 右图为weakly correlated.

　　Normalization的过程主要和统计学相关，也就说加试和个人的成绩并无任何关系，即使不做也是不算分的，然而考生的个人加试成绩会影响总体的数值，对所有考生的成绩同时产生影响。最后3点启示：

　　1.当你报考的考试日里大部分人都看到了命中的机经，整个成绩会negatively skewed, 你的成绩会比raw score要低，当你报考的考试日出现了没有看过的题目，大部分人的成绩可能不够好，整个成绩会positively skewed，你的成绩会比raw score要高。

　　2.加试部分的特点是多次重复并已经被分析过，中国的"经典加试"就是normalizing的部分，并不存在所谓的"不知道哪一部分是加试"的说法。

　　3.ETS明确表示Equating cannot adjust scores correctly for every individual test-taker，也就意味着该过程对总体负责，但对个人成绩可能有所偏差。

　　NOTE:

　　Angoff, W. H. (1984). Scales, norms, and equivalent scores. Princeton, NJ: Educational Testing Service.

　　Holland, P. W., & Thayer, D. T. (1987). Notes on the use of log-linear models for fitting discrete probability distributions (Program Statistics Research Technical Report No. 87-79). Princeton, NJ: Educational Testing Service.

　　Holland, P. W., & Thayer, D. T. (1989). The kernel method of equating score distributions (Program Statistics Research Technical Report No. 89-84). Princeton, NJ: Educational Testing Service.

　　Holland, P. W., & Thayer, D. T. (2000). Univariate and bivariate loglinear models for discrete test score distributions. Journal of Educational and Behavioral Statistics, 25(2), 133-183.

　　Kolen, M. J. (1991). Smoothing methods for estimating test score distributions. Journal of Educational Measurement, 28, 257-282.

　　Kolen, M. J., & Brennan, R. L. (1995). Test equating. New York: Springer.

　　Liou, M., & Cheng, P. E. (1995). A symptotic standard error of equipercentile equating. Journal of Educational and Behavioral Statistics, 20(3), 259-286.

　　Livingston, S. A. (1993). Small-sample equating with log-linear smoothing. Journal of Educational Measurement, 30, 23-39.

　　Livingston, S. A., Dorans, N. J., & Wright, N. K. (1990). What combination of sampling and equating methods works best? Applied Measurement in Education, 3(1), 73-95.

　　Lord, F. M. (1980). Applications of item response theory to practical testing problems. Hillsdale, NJ: Lawrence Erlbaum Associates.